Bienvenidos a Mi blog:
Mi nombre es Maria del Pilar Huerta Ramos
Aqui les presento una sintesis sobre el Algebra Lineal y las matrices.
Espero que les ayude a Comprender y Aprender.
Aprendamos a Colaborar, a Buscar y a Enseñar.
Espero que les ayude a Comprender y Aprender.
Aprendamos a Colaborar, a Buscar y a Enseñar.
Ese es el objetivo de este Blog, Conocer los conceptos y propiedades principales de los sistemas lineales y las matrices.
ALGEBRA LINEAL
El álgebra lineal es la rama de las matemáticas que estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales, y sus transformaciones lineales.
Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.
La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann publicó su libro Die lineare Ausdehnungslehre (La teoría lineal de extensión)
http://es.wikipedia.org/wiki/%C3%81lgebra_lineal
http://es.wikipedia.org/wiki/%C3%81lgebra_lineal
En el siguiente Link, encontramos unos apuntes de ALGEBRA LINEAL: Juan González-Meneses López. / Curso 2008/2009
Estos apuntes ayudaran a comprender el Algebra Lineal, es un Trabajo bien elaborado y util para la materia.
SISTEMAS LINEALES
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
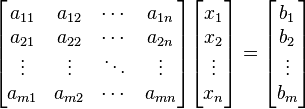
En general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:
Donde
 son las incógnitas y los números
son las incógnitas y los números  son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/wikipedia/es/math/d/1/4/d14d1db377877372695cb6ca4559a1d4.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:(1)Si representamos cada matriz con una única letra obtenemos:
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del que provengan los coeficientes.
PRESENTACION PHOTOPEACH SISTEMAS LINEALES
Ecuaciones Lineales con PhotoPeach
A continuación tenemos un video elaborado por La economista : Ana Abad Para la Universidad Tecnica Particular de Loja (UTPL)
Este video contiene información de algebra lineal sobre los temas de: Sistemas Lineales, Matrices y Vectores.
CONCEPTO DE MATRIZ
En matemáticas, una matriz es un arreglo bidimensional de números, y en su mayor generalidad de elementos de un anillo. Las matrices se usan generalmente para describir sistemas de ecuaciones lineales, sistemas de ecuaciones diferenciales o representar una aplicación lineal (dada una base). Las matrices se describen en el campo de la teoría de matrices.
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar las aplicaciones lineales; en este último caso las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
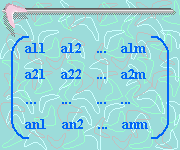
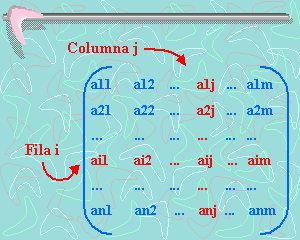
Llamaremos
matriz de orden (nxm)
sobre el cuerpo de los números reales a un conjunto de números reales
dispuestos en n filas y m columnas de la siguiente forma:
Consideraciones
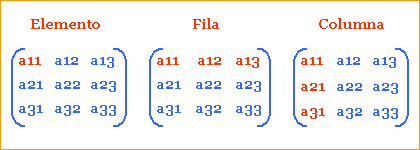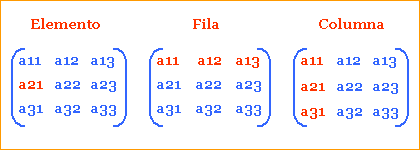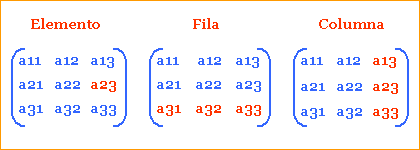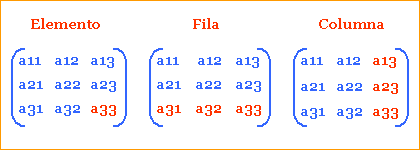
1. Las matrices se designan con
una letra mayúscula, como A, B, C , D , etc.
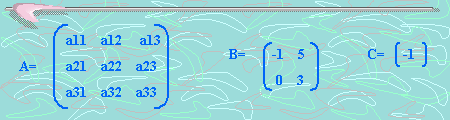
Ejemplo:
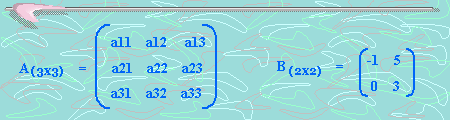
2. La dimensión u orden de una
matriz, está dado por la cantidad de filas (n) y la
cantidad de columnas (m) que esta tenga y se denota por (nxm).
Ejemplo:
3. Cada elemento de la matriz
corresponde a un número real representado de la forma (aij) donde
i corresponde a la posición de fila y j
corresponde a la posición de la columna dentro de la matriz.
Ejemplo:
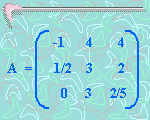
Donde:

4. La cantidad de elementos de la
matriz se determina multiplicando la cantidad de filas
por la cantidad de columnas.
Ejemplo:
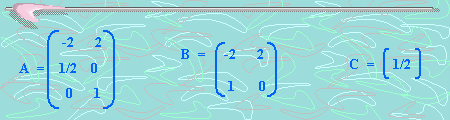
De ahora en adelante, denotaremos
por A(nxm) o simplemente A, a una matriz cualquiera de
orden (nxm) con elementos pertenecientes a los números
reales.
MATRICES IGUALES
Diremos que dos matrices son
iguales, si tienen el mismo orden o dimensión y los
elementos que se encuentran en la misma posición,
son iguales. Esto es:

La idea es que dos matrices son
diferentes si difieren en al menos un elemento.
Ejemplo:

Luego, A = B.
Suma o adición de matrices
Sean  . Se define la operación de adición de matrices como una operación bianria
. Se define la operación de adición de matrices como una operación bianria  tal que
tal que  y donde
y donde  en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo
en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo  . Por ejemplo, la entrada
. Por ejemplo, la entrada  es igual a la suma de los elementos
es igual a la suma de los elementos  y
y  lo cual es
lo cual es  .
.
 . Se define la operación de adición de matrices como una operación bianria
. Se define la operación de adición de matrices como una operación bianria  tal que
tal que  y donde
y donde  en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo
en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo  . Por ejemplo, la entrada
. Por ejemplo, la entrada  es igual a la suma de los elementos
es igual a la suma de los elementos  y
y  lo cual es
lo cual es  .
.
Veamos un ejemplo más explícito. Sea 

A la luz de éstos ejemplos es inmediato ver que dos matrices se
pueden sumar solamente si ambas tienen el mismo tamaño. La suma de
matrices en el caso de que las entradas estén en un campo serán
la asociatividad, la conmutatividad, existencia de elemento neutro
aditivo y existencia de inverso aditivo. Ésto es así ya que éstas son
propiedades de los campos en los que están las entradas de la matriz.













Suma
y resta de matrices
Para poder sumar o restar matrices,
éstas deben tener el mismo número de filas y de columnas. Es decir, si
una matriz es de orden 3 ´ 2 y otra de 3 ´ 3, no se pueden sumar ni restar.
Esto es así ya que, tanto para la suma como para la resta, se suman o
se restan los términos que ocupan el mismo lugar en las matrices.
Ejemplo:








Para sumar o restar más de dos
matrices se procede igual. No necesariamente para poder sumar o restar
matrices, éstas tienen que ser cuadradas.
Ejemplo:
A continuación tenemos un video de la suma y Resta de matrices. Elaborado por Juanmemo
En este vídeo se calcula la suma de dos matrices:MUTIPLICACION DE MATRICES
En matemática, la multiplicación o producto de matrices es la operación de composición efectuada entre dos matrices, o bien la multiplicación entre una matriz y un escalar según unas reglas.
Al igual que la multiplicación aritmética, su definición es instrumental, es decir, viene dada por un algoritmo capaz de efectuarla. El algoritmo para la multiplicación matricial es diferente del que resuelve la multiplicación de dos números. La diferencia principal es que la multiplicación de matrices no cumple con la propiedad de conmutatividad.
Multiplicación de una matriz por un escalar:
Dada una matriz A de m filas y n columnas es una matriz del tipo: que se escribe genericamente como
que se escribe genericamente como 
 que se escribe genericamente como
que se escribe genericamente como 
Propiedades
Sean A, B matrices y c, d escalares, la multiplicación de matrices por escalares cumple con las siguientes propiedades:| Propiedad | Descripción |
| Clausura | cA es también una matriz |
| Elemento neutro | Existe el elemento neutro uno, de manera que 1·A = A |
| Propiedad asociativa | (cd)A = c(dA) |
| Propiedad distributiva - De escalar - De matriz |
c(A+B) = cA+cB (c+d)A = cA+dA |
Multiplicación de una matriz por otra matriz
 y
y 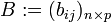
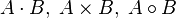 o simplemente AB, el resultado del producto es una nueva matriz C:
o simplemente AB, el resultado del producto es una nueva matriz C:A continuacion tenemos un video elaborado por el Profesor Julio Rios de Colombia sobre LA MULTIPLICACION DE MATRICES:
MATRIZ INVERSA
Dada una matriz A, ¿Podremos encontrar otra matriz B tal que A·B=B·A=I?
Esta matriz B existe aunque no siempre, de existir se le llama matriz inversa de A y se nota A-1. Para que exista la inversa de A, ésta tiene que ser cuadrada pues de lo contrario no se podría hacer el producto por la izquierda y por la derecha, luego cuando hablamos de matrices invertibles estamos hablando de matrices cuadradas.
Condición necesaria y suficiente para que una matriz sea invertible
es que no sea singular, es decir, que su determinante sea no nulo |A|
≠ 0
Cálculo de la matriz inversa
1. Método de Gauss-Jordan
Este método consiste en colocar junto a la matriz de partida (A) la matriz identidad (I) y hacer operaciones por filas, afectando esas operaciones tanto a A como a I, con el objeto de transformar la matriz A en la matriz identidad, la matriz resultante de las operaciones sobre I es la inversa de A (A-1).
Las operaciones que podemos hacer sobre las filas son:
a) Sustituir una fila por ella multiplicada por una constante, por ejemplo, sustituimos la fila 2 por ella multiplicada por 3.
b) Permutar dos filas
c) Sustituir una fila por una combinación lineal de ella y otras.

La matriz inversa de A es

A continuacion tenemos un video elaborado Por Unicoos / Matematicas Sobre La matriz inversa por el Método de Gauss Jordan:
Ejercicios de Sistemas de Ecuaciones
Ejercicios de Matrices
Determinante (matemática)
En Matemáticas se define el determinante como una forma multilineal alternada
de un cuerpo. Esta definición indica una serie de propiedades
matemáticas y generaliza el concepto de determinante haciéndolo
aplicable en numerosos campos. Sin embargo, el concepto de determinante o
de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.
Métodos de cálculo
Para el cálculo de determinantes de matrices de cualquier orden,
existe una regla recursiva (teorema de Laplace) que reduce el cálculo a
sumas y restas de varios determinantes de un orden inferior. Este
proceso se puede repetir tantas veces como sea necesario hasta reducir
el problema al cálculo de múltiples determinantes de orden tan pequeño
como se quiera. Sabiendo que el determinante de un escalar es el propio
escalar, es posible calcular el determinante de cualquier matriz
aplicando dicho teorema.
Además de esta regla, para calcular determinantes de matrices de
cualquier orden podemos usar otra definición de determinante conocida
como Fórmula de Leibniz.
La fórmula de Leibniz para el determinante de una matriz cuadrada A de orden n es:
donde la suma se calcula sobre todas las permutaciónes σ del conjunto {1,2,...,n}. La posición del elemento i después de la permutación σ se denota como σi. El conjunto de todas las permutaciones es Pn. Para cada σ, sgn(σ) es la signatura de σ, esto es +1 si la permutación es par y −1 si es impar (ver Paridad de permutaciones).
En cualquiera de los 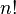 sumandos, el término
sumandos, el término
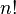 sumandos, el término
sumandos, el término
denota el producto de las entradas en la posición (i, σi), donde i va desde 1 hasta n:
La fórmula de Leibniz es útil como definición de determinante; pero,
excepto en casos muy pequeños, no es una forma práctica de calcularlo:
hay que llevar a cabo n! productos de n factores y sumar n! elementos.
No se suele usar para calcular el determinante si la matriz tiene más de
tres filas.
Matrices de orden inferior
El caso de matrices de orden inferior (orden 1, 2 ó 3) es tan
sencillo que su determinante se calcula con sencillas reglas conocidas.
Dichas reglas son también deducibles del teorema de Laplace.
Una matriz de orden uno, es un caso trivial, pero lo trataremos para
completar todos los casos. Una matriz de orden uno puede ser tratada
como un escalar, pero aquí la consideraremos una matriz cuadrada de
orden uno:
El valor del determinante es igual al único termino de la matriz:
Los determinantes de una matriz de orden 2:
se calculan con la siguiente fórmula:
Dada una matriz de orden 3:
En determinante de orden 3 se calcula mediante la regla de Sarrus:
Determinantes de orden superior
El determinante de orden n, puede desarrollarse a partir de una fila o
columna, reduciendo el problema al cálculo de un determinante de orden
n-1. Para ello se toma una fila o columna cualquiera, multiplicando cada
elemento por su cofactor (es decir, el determinante de la matriz que se
obtiene eliminando la fila y columna correspondiente a dicho elemento,
multiplicado por (-1)i+j donde i es el número de fila y j el número de columna). La suma de todos los productos es igual al determinante.
En caso de un determinante de orden 4, se obtienen directamente
determinantes de orden 3 que podrán ser calculados por la regla de
Sarrus. En cambio, en los determinantes de orden superior, como por
ejemplo n = 5, al desarrollar los elementos de una línea, obtendremos
determinantes de orden 4, que a su vez se deberán desarrollar en por el
mismo método, para obtener determinantes de orden 3. Por ejemplo, para
obtener con el método especificado un determinante de orden 4, se deben
calcular 4 determinantes de orden 3. En cambio, si previamente se logran
tres ceros en una fila o columna, bastara con calcular solo un
determinante de orden 3 (ya que los demás determinantes estarán
multiplicados por 0, lo que los anula).
La cantidad de operaciones aumenta muy rápidamente. En el peor de los
casos (sin obtener ceros en filas y columnas), para un determinante de
orden 4 se deberán desarrollar 4 determinates de orden 3. En un
determinante de orden 5, se obtienen 5 determinates de orden 4 a
desarrollar, dándonos 20 determinates de orden 3. El número de
determinates de orden 3 que se obtienen en el desarrollo de un
determinante de orden n es igual a 

Por ejemplo, mediante este método, para un determinante de orden 10
se deberán calcular 10 x 9 x 8 x 7 x 6 x 5 x 4 = 604.800 determinantes
de orden 3.
También puede utilizarse el Método de eliminación Gaussiana, para
convertir la matriz en una matriz triangular. Si bien el proceso puede
parecer tedioso, estará muy lejos de los 14.529.715.200 de determinantes
de orden 3 necesarios para calcular el determinante de una matriz de
orden 14.
Métodos numéricos
Para reducir el coste computacional de los determinantes a la vez que
mejorar su estabilidad frente a errores de redondeo, se aplica la regla de Chio,
que permite utilizar métodos de triangularización de la matriz
reduciendo con ello el cálculo del determinante al producto de los
elementos de la diagonal de la matriz resultante. Para la
triangularización se puede utilizar cualquier método conocido que sea
numéricamente estable. Éstos suelen basarse en el uso de matrices
ortonormales, como ocurre con el método de Gauss o con el uso de reflexiones de Householder o rotaciones de Givens.
La precisión limitada del cálculo numérico produce incertidumbre en
ocasiones en los resultados de este método. Un valor muy pequeño del
determinante podría ser el resultado de una matriz de rango deficiente,
aunque no lo es necesariamente. Por otra parte, para matrices casi
singulares el resultado no siempre es preciso. Es necesario comprobar el
rango de la matriz con otros métodos o calcular el número de condición de la matriz para determinar la fiabilidad del resultado.
Determinantes en dimensión infinita
Bajo ciertas condiciones puede definirse el determinante de aplicaciones lineales de un espacio vectorial de Banach de dimensión infinita. En concreto en el determinante está definido para los operades de la clase de determinante que puede a partir de los operadores de la clase de traza. Un ejemplo notable fue el determinante de Fredholm que éste definió en conexión con su estudio de la ecuación integral que lleva su nombre:
(*)
Donde:
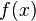 es una función conocida
es una función conocida es una la función incógnita
es una la función incógnita es una función conocida llamada núcleo, que da lugar al siguiente
operador lineal compacto y de traza finita en el espacio de Hilbert de funciones de cuadrado integrable en el intervalo [0,1]:
es una función conocida llamada núcleo, que da lugar al siguiente
operador lineal compacto y de traza finita en el espacio de Hilbert de funciones de cuadrado integrable en el intervalo [0,1]:
:
La ecuación () tiene solución si el determinante de Fredholm  no se anula. El determinante de Fredholm en este caso generaliza al
determinante en dimensión finita y puede calcularse explícitamente
mediante:
no se anula. El determinante de Fredholm en este caso generaliza al
determinante en dimensión finita y puede calcularse explícitamente
mediante:
 no se anula. El determinante de Fredholm en este caso generaliza al
determinante en dimensión finita y puede calcularse explícitamente
mediante:
no se anula. El determinante de Fredholm en este caso generaliza al
determinante en dimensión finita y puede calcularse explícitamente
mediante:
La propia solcuión de la ecuación () puede escribirse de manera simple en términos del determinante cuando este no se anula.
Primeros ejemplos: áreas y volúmenes
El cálculo de áreas y volúmenes bajo forma de determinantes en espacios euclídeos
aparecen como casos particulares de una noción más general de
determinante. La letra mayúscula D (Det) se reserva a veces para
distinguirlos.
Determinante de dos vectores en el plano euclídeo
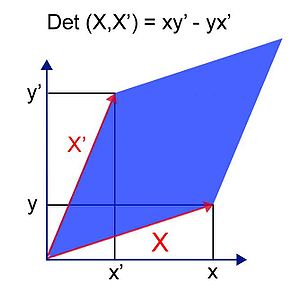
Sea P el plano euclídeo. El determinante de los vectores X y X' se obtiene con la expresión analítica
o, de manera equivalente, por la expresión geométrica
en la cual  es el ángulo orientado formado por los vectores X y X'.
es el ángulo orientado formado por los vectores X y X'.
 es el ángulo orientado formado por los vectores X y X'.
es el ángulo orientado formado por los vectores X y X'.Propiedades
- El valor absoluto del determinante es igual a la superficie del paralelogramo definido por X y X' (
 es en efecto la altura del paralelogramo, por lo que A = Base × Altura).
es en efecto la altura del paralelogramo, por lo que A = Base × Altura). - El determinante es nulo si y sólo si los dos vectores son colineales (el paralelogramo se convierte en una línea).
- Su signo es estrictamente positivo si y sólo si la medida del ángulo (X, X ') se encuentra en ]0,
 [.
[. - La aplicación del determinante es bilineal: la linearidad respecto al primer vector se escribe
y respecto al segundo
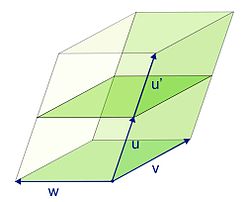
La figura 2, en el plano, ilustra un caso particular de esta fórmula.
Representa dos paralelogramos adyacentes, uno definido por los vectores
u y v (en verde), y otro por los vectores u' y v (en azul). Es fácil
ver sobre este ejemplo el área del paralelogramo definido por los
vectores u+u' y v (en gris): es igual a la suma de los dos
paralelogramos precedentes a la cual se sustrae el área de un triángulo y
se añade el área de otro triángulo. Ambos triángulos se corresponden
por translación y la fórmula siguiente se verifica Det (u+u', v)=Det (u,
v)+Det (u', v).
El dibujo corresponde a un caso particular de la fórmula de
bilinealidad ya que las orientaciones han sido elegidas de manera que
las áreas tengan el mismo signo, aunque ayuda a comprender el contenido
geométrico.
Generalización
Es posible definir la noción de determinante en un plano euclídeo orientado con una base ortonormal directa B
utilizando las coordenadas de los vectores en esta base. El cálculo del
determinante da el mismo resultado sea cual sea la base ortonormal
directa elegida para el cálculo.
Determinante de tres vectores en el espacio euclídeo
Sea E el espacio euclídeo orientado de dimensión 3. El determinante de tres vectores de E se da por
Este determinante lleva el nombre de producto mixto.
Propiedades
- El valor absoluto del determinante es igual al volumen de paralelepípedo definido por los tres vectores.
- El determinante es nulo si y sólo si los tres vectores se encuentran en un mismo plano (paralelepípedo "plano").
- La aplicación determinante es trilineal: sobre todo
Una ilustración geométrica de esta propiedad se da en la figura 3 con
dos paralelepípedos adyacentes, es decir con una cara común. La
igualdad siguiente es entonces intuitiva:
 .
.
Propiedades
- El determinante de una matriz es un invariante algebraico, lo cual implica que dada una aplicación lineal todas las matrices que la represente tendrán el mismo determinante. Eso permite definir el valor del determinante no sólo para matrices sino también para aplicaciones lineales.
- El determinante de una matriz y el de su traspuesta coinciden:

- Una aplicación lineal entre espacios vectoriales es invertible si y sólo si su determinante no es nulo. Por lo tanto, una matriz con coeficientes en un cuerpo es invertible si y sólo si su determinante es no nulo.
Determinante del producto
- Una propiedad fundamental del determinante es su comportamiento multiplicativo frente al producto de matrices:
Esta propiedad es más trascendente de lo que parece y es muy útil en
el cálculo de determinantes. En efecto, supongamos que queremos calcular
el determinante de la matriz 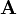 y que
y que 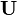 es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
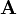 y que
y que 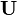 es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
Una aplicación lineal entre dos espacios vectoriales de dimensión
finita se puede representar mediante una matriz. La matriz asociada a la
composición
de aplicaciones lineales entre espacios de dimensión finita se puede
calcular mediante el producto de matrices. Dadas dos aplicaciones
lineales  y
y  , se cumple lo siguiente:
, se cumple lo siguiente:
 y
y  , se cumple lo siguiente:
, se cumple lo siguiente:
A continuacion tenemos un video elaborado Por marcelrzmuo
Sobre el
Calculo de determinantes para matriz de 3x3
A continuacion tenemos un video elaborado Por 2º BACHI unicoos Sobre la Resolucion de un DETERMINANTE 4X4 utilizando adjuntos (o cofactores),
tambien llamado Metodo de LAPLACE. Para ello, deberemos elegir la fila o
oclumna por la que queremos
A continuacion tenemos un video elaborado Por marcelrzmuo
Sobre Como calcular el determinante de una matriz cuadrada de 3x3 por sarrus
Muchas Gracias por ingresar al Blog Conociendo las matemáticas.
Que tengan un Lindo dia.


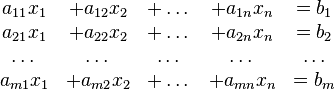
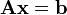











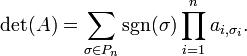
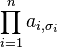



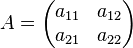





![\det(I+\hat{K}) = \sum_{k=0}^\infty \frac{1}{k!}\int_0^1\dots\int_0^1
\det[K(x_i,x_j)]_{1\le i, j \le k}\ dx_1\dots dx_k](http://upload.wikimedia.org/math/a/d/3/ad39f03c0adafbe3c5024fc8236d0a41.png)









No hay comentarios:
Publicar un comentario